【LoL】一番かたくなるHPとAR(orMR)配分についての検証

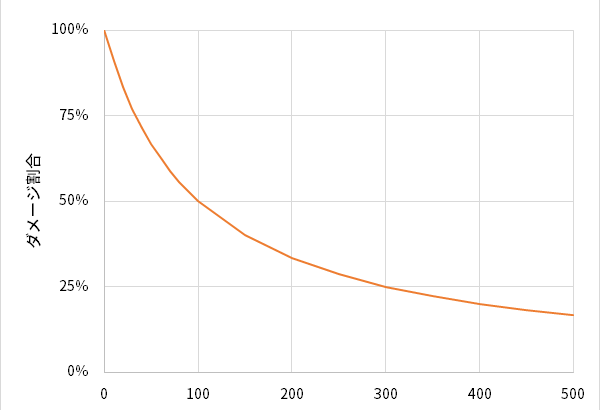
この記事の内容を3行で

かたくなるための最適なHPとAR配分は?

だいぶ間が空いてしましましたが、今回のテーマは「かたくなるための最適なHPとAR(orMR)の配分」です。

ダメージを出そうとするビルドはある意味単純です。自分に必要なADorAPをひたすらに積めばいいからです。しかし、タンクビルドはHPとARとMRを選んで積む必要があります。相手が全て物理攻撃系のチャンピオンだったとしてもHPを積むかARを積むかは悩みどころです。とは言え、ビルドは基本的にはop.ggなどから真似をするのが間違いありません。そういう意味では悩む必要は無いのですが、例えば相手チームがオールAP構成、つまり魔法攻撃主体のチームのようなレアケースに当たった場合を考えてみます。それでもいつも通りの一般的なビルドに行くという選択肢もありますが、それから少し離れてMRをいつもより多めに積む、という選択肢もあります。そんな、自分でビルドを考えなければいけない場合にこの知識の出番です。

もしかしたらHPはARの7.5倍が一番かたくなる、などこの知識自体は知っている人も多いかもしれません。しかし、なんで7.5倍になるのか数字の根拠まで知っている人は少ないのではないでしょうか。実際、自分が調べようと思って検索してもあまりヒットしませんでした。というわけで、この記事ではなんで物理攻撃に一番かたいのがHP=750+AR×7.5になり、魔法攻撃に一番かたいのがHP=675+MR×6.75であるのかをステータス計算式などを使って説明していきます。

ゴールドのせいでHPとARは無限に上げられない

まず、前提としてステータスはゴールドによる縛りがあるということです。さっきからHPとARの数字について言及してますが、一番かたいのはとにかく数字が大きい9999HPと999ARです。でも実際のゲーム中はゴールドでアイテムを買ってステータスを上昇させます。また、アイテムは6個までしか持てないので、HPとARを両方とも無限に上げるということはできません。ゲーム中はゴールドによる制限、フルビルドでもアイテムの上限によって、どちらかを上げる、またはHPとARをバランスよく上げることになります。今回の主題はこのバランスについてどうすべきかということを検討します。

次に、一番かたいとは一番エフェクティブHPが多い、ということです。エフェクティブHPについてはこの記事で詳しく説明しています。ここで簡単に説明すると異なったHPとARでもかたさを比較できる数字です。その値はそのHPとARで実現できている同じかたさを0ARの時にどれだけのHPがあれば同じかたさになるかを示しています。例えば、1500HPと0AR、1000HPと50AR、750HPと100ARは全て同じ1500エフェクティブHPです。エフェクティブHPは物理攻撃と魔法攻撃のそれぞれ別に計算します。以下では物理攻撃のみに注目して話を進めます。魔法攻撃に関しては一通り説明が終わった後に触れますが、数字が違うだけで考え方は原則的にはほとんど同じです。必要ならばARをMRに適宜読み替えても、問題ありません。

エフェクティブHPは以下の式で計算できます。以下の式ではエフェクティブHPはEHPと表現しています。

$$EHP = HP \times (1+ \frac{1}{100}\ AR)$$

ゴールドとステータスをつなげるゴールド効率

上記のとおりHPとARはゴールドによって制限を受けます。使ったゴールドとステータスの値はゴールド効率を使って変換できます。（ゴールド効率の詳細についてはこの記事をご覧ください。）今話題にしているゴールド効率はそれぞれ、HPは2.67ゴールドを使うとHPが1増え、ARは20ゴールドを使うと1AR増えます。（MRは18ゴールドを使うと1MR増えます。）ここで、HPとARに使うことが出来るゴールド量をGとおき、HPに使うゴールド量をxと置きます。すると、投じたゴールド量とHPとARの関係は以下の式のようになります。

$$HP = \frac {x} {2.67}\ $$

$$AR = \frac {(G-x)} {20}\ $$

上記のステータスとゴールドの関係式をエフェクティブHPの式に代入すると以下の式になります。

$$EHP = \frac {x} {2.67}\ \times (1+ \frac{1}{100}\ \times \frac {(G-x)} {20}\ )$$

そして、エフェクティブHPとHPに使うゴールド量xの関係式を展開します。

後はひたすら式変形

後はひたすら中学や高校の数学みたいな式変形をするだけです。

$$EHP = \frac {x} {2.67}\ \times (1+ \frac{1}{100}\ \times \frac {(G-x)} {20}\ )$$

$$EHP = \frac {1} {2.67}\ \times (x+ \frac{G}{2000}\ x – \frac {1} {2000}\ x^2 )$$

$$EHP = -\frac {2000} {2.67}\ \times (-2000x – Gx + x^2)$$

$$EHP = -\frac {2000} {2.67}\ \times (x^2 – (2000 + G)x)$$

$$EHP = -\frac {2000} {2.67}\ \times \{(x – \frac {2000 + G}{2}\ )^2 – ( \frac{2000 + G}{2}\ )^2 \} $$

これで、この式はxに関しての二次関数であることがわかりました。平方完成もできたので、xが$$ \frac {2000 + G}{2}\ = \frac {1}{2}\ G +1000 $$の時に最大になることがわかります。xはHPにかけるお金で、値はエフェクティブHPを表しているので、HPにこれだけのお金をかけたときにエフェクティブHPが最大になることがわかりました。残りのお金、つまりARに使う金額は$$ \frac {1}{2}\ G -1000 $$です。上記の値を言葉で表現すると、HPとARに使う金額を半分にした後、1000ゴールドをARからHPに移す、という分け方です。別の表現をすると使えるゴールドのうち、まず2000ゴールドをHPに使い、残りをHPとARに半分づつ使う、とも言えます。

これで、一番物理攻撃に対してかたくなる金額の使い方がわかりました。しかし、実際に使った金額というものかなりわかりにくいです。当然、ステータスに投じた金額を計算することも面倒くさいです。そこでわかりやすく各ステータスのゴールド効率を使ってステータスに直しまます。

まずはHPに使う2000ゴールドはHP換算するといくつかを考えます。繰り返しになりますがHPは2.67ゴールドを使うとHPが1増えるので、2000÷2.67=750です。そして、残りの金額をHPとARに同じだけの金額をステータスに投じます。これは、ゴールド効率の逆数の比がそのままステータスの比になります。つまり、以下のようになります。

$$HP:AR= \frac {1}{2.67}\ : \frac {1}{20}\ =7.5:1$$

HPとARに同じだけの金額を使うとHPとARはHPがARの7.5倍になることがわかりました。これですべて終わりです。つまりこれがゴールドが限られている場合のエフェクティブHPを最大にするHPとARの振り方です。

まとめると、HPはARの7.5倍に750を足した値になっているようにするのが、エフェクティブHPを最大にするHPとARのバランスです。式でHPとARの関係を表すと以下のように書けます。

$$HP=750+AR \times 7.5$$

MRに関しても数字が全く同じ展開

MRに関しても数字が違うだけで方法は全く同じです。同じ式の展開なので最初と最後のみ示します。

$$AR = \frac {(G-x)} {18}\ $$

$$EHP = \frac {x} {2.67}\ \times (1+ \frac{1}{100}\ \times \frac {(G-x)} {18}\ )$$

$$EHP = -\frac {1800} {2.67}\ \times \{(x – \frac {1800 + G}{2}\ )^2 – ( \frac{1800 + G}{2}\ )^2 \} $$

物理の場合と同様に言い換えると、1800ゴールドはHPに使い、残りをHPとARに半分づつ使います。これをステータスに直します。

$$HP:MR= \frac {1}{2.67}\ : \frac {1}{18}\ =6.75:1$$

1800ゴールドのHPは675で、同じ金額をHPとMRに使ったなら、HPはMRの6.75倍の値になります。よって魔法攻撃に対して一番エフェクティブHPが大きくなるHPとMRの関係は以下のようになります。

$$HP=675+AR \times 6.75$$

念のためですがこれはチャンピオンの基礎ステータスとアイテムの増加ステータスを合わせた数字です。

序盤はHP、中盤以降にAR

全てのチャンピオンの基礎ステータスは上記の基準からすると序盤はHPが足りず、レベルが上がると、AR(orMR)が足りない状態になります。なので序盤、たいていはHPが1000を超えるぐらいまではHPアイテムを買い、それ以降、足りないAR(orMR)を買い足す、という感じになります。特に、タンクアイテムを買う場合に、素材アイテムを買う順番を決めるときにが一番使いやすいです。たいていのタンクアイテムはHPとAR(orMR)の両方がもらえますが、中間アイテムはどちらかしかもらえないことが多いです。どちらの素材や中間アイテムを買えばより硬くなるかを意識して買えばHP1で残れることが多くなるかもしれません。

HPリジェネやライフスティールも考慮に入れてバランスをとる

今回の議論は単純化するためにHPとAR(orMR)のみに注目しました。実際のゲーム中はHPリジェネやシールド、ライフスティールなど、HPそのものではないが、HPが多くなっているとみなせる状況もあります。逆にスキルの効果でARやMRが上がる場合もあります。HPが多くなっているとみなせるならば基準より多くのAR(orMR)を積むのがいいですし、逆にARやMRが上がっているタイミングを重視するならよりHPを積むべきです。その場合はどれだけ積むべきか、となると難しい問題になります。しかし、理論値を求めるのがむずかしいだけで、実際はビルドサイトなどをみながら考えて選べばいいだけです。

さらに、今回の話は物理攻撃と魔法攻撃を別々に考えています。実際は両方の攻撃と固定ダメージの攻撃も飛んでくるので、全てに対して対応しようとするとこれまた難しくなります。一般的に言えることは、ARは物理攻撃のみ軽減し、MRは魔法攻撃のみを軽減するのに対して、HPは物理、魔法、固定ダメージの全てに対応できる、ということです。だから、全てに対応しようとするならば基準よりHPを多めにすることになりますが、そもそも、全てに対応しようとする方針が正しいのか?という問題もあります。これも結局はビルドサイトを参照をするのが勝ちやすい方法です。

たまにちょっとだけ使う知識

今回の記事ではHP=AR×7.5+750のときに物理攻撃に、HP=MR×6.75+675のときに魔法攻撃に対して一番かたくなる、ということを数式を使って説明、証明しました。しかし、実際のゲームではそれ以外の要素も多く、この比率はあくまで基本的なもの考え方のベースになるものです。結局、こんなめんどくさいことを考えなくてもビルドサイトを参照を参照すればいいじゃん、というのはその通りです。だからこの知識は、基本的には毎ゲーム使うようなものではなく、ビルドを検討するときや、ゲーム中にいつも通りのビルドをしているときにたまに確認してみるなど、たまにちょっとだけ使う知識です。実際のゲーム中に、直接この知識が必要な場面は少ないでしょうが、普段から使っているアイテムビルドをこの知識を通して見てみるとまた新たな発見や気づきがあるんじゃないかと思います。

結論を3行で