【LoL】時間ごとのゴールド差と勝率の相関関係について

実験データの概要：集計したデータに関して

実験について、まずは今回集めたデータに関して概要を示します。RiotAPIを使い、パッチ11.7から11.10の日本サーバーで行われたランクマッチ約40万ゲームを集計しました。RiotAPIでは1マッチの1分毎にゴールドデータが取得できます。そこで、1分毎、1000G毎に区切り勝ち負け数を集計し、勝率を計算しました。

実験1の結果：ゴールド差ごとの時間変化による勝率の変化グラフ

上記データをまとめ、折れ線グラフに表したものが図2です。

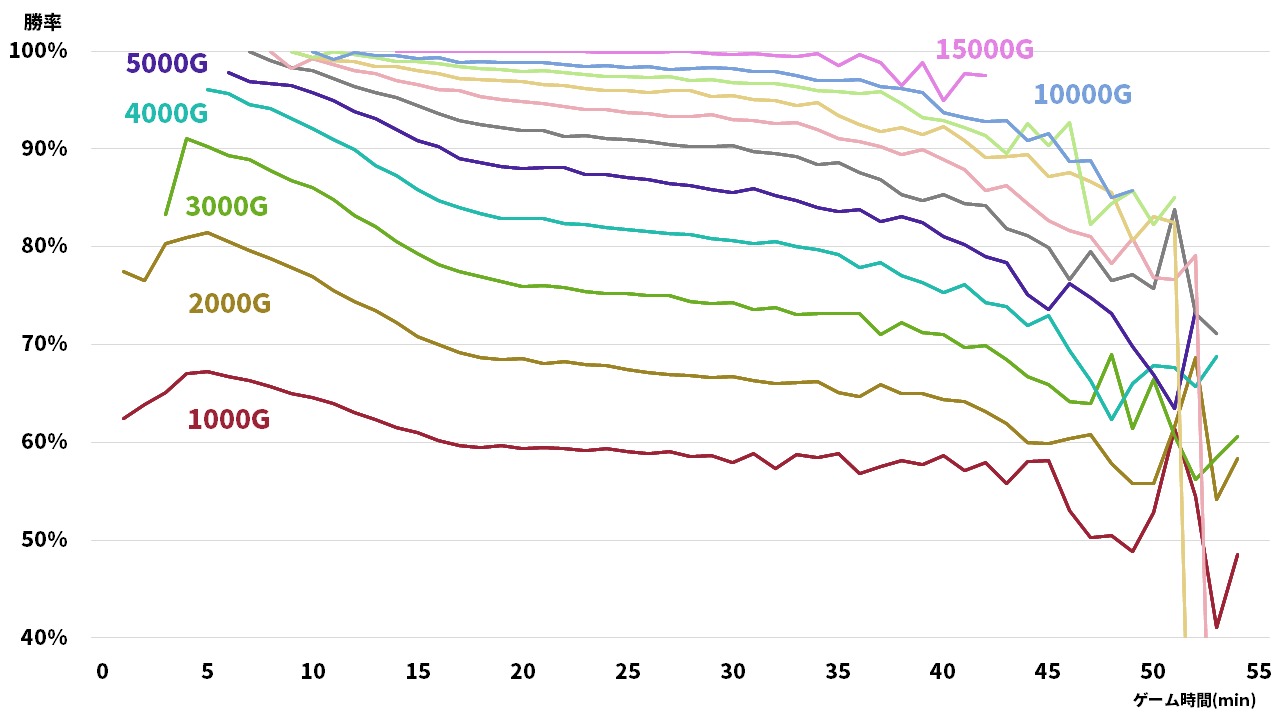
横軸がゲーム時間、縦軸が勝率で、折れ線グラフの系列それぞれがゴールド差ごとのグラフになっています。一番下の赤い折れ線グラフが1000G差の勝率です。それから上に黄色の2000G、緑の3000Gと1000Gづつで、最後から2番目が水色の10000G、一番上は5000G飛んで、薄紫の15000Gのグラフになっています。間の11000Gから14000Gや16000G以上のグラフもありますが、見やすさの都合上省いてあります。
まず、大前提としてゴールド差があればあるほど勝率がちゃんと高くなっているということです。そして目につくのが、上の方が折れ線グラフの間隔が狭いということです。これはゴールド差があればあるほど、勝率は上がるものの勝率の上がり幅は小さくなる、ということです。そして、全てのグラフが右肩下がりになっています。これは同じゴールド差であれば、時間がたてばたつほど勝率が悪くなることを示しています。下がり方に関して、17~18分ごろに傾きが変化し、それまで急だったものがなだらかになっています。この原因に関しては不明です。この時間帯にあることは、15分からできる早期サレンダー、多くの場合は3体目のドラゴンや2匹目のリフトヘラルドなどがありますが関連はわかりません。次に、40分以降に注目すると、グラフが交差するようになります。これは、40分以前ではゴールド差が大きければ大きいほど勝率が高かったですが、40分以降の時間帯からそうではないことが表れています。

実験1の議論：グラフの意義

改めて、グラフから得られた結果を箇条書きでまとめると以下のようになります。

これらの事実は、はっきり言って目新しさはないですが、今まで定性的に語られていたことが集めたデータと矛盾していない、つじつまが合っていることが重要だと考えています。このことから、今回のデータは信頼性があると考えています。
このグラフは、ゴールド差という非常に一般的な指標と、勝率が対応させ、可視化した点が面白い部分だと考えています。一方で、これはゴールド差しか評価していません。LoLの勝ち負けにはオブジェクトやドラゴン、パワースパイクの違うチャンピオンなどまだまだ無数の要素があります。今回のグラフはこれらは全く考慮していません。つまりこのグラフは、ゴールド差以外の要素が平均的な状態にあると仮定しています。状況によってはかなり勝率が違うときもあることが考えられますが、その具体的な状況や勝率は現状ではわからないので、今後の課題だと考えています。

実験2の結果：31分以降の勝ち負け数についてのカイ二乗検定

次に、ゴールド差が勝率の違いに現れなくなる時間帯はいつからか、という問題を検討していきます。図2のグラフでは40分以降の時間帯から系列が交差している部分があります。例えば45分ごろ、うす緑の9000G差と水色の10000G差の部分です。これは、この時間帯はすでに9000G差と10000G差では勝率に殆ど違いがないということを示しています。そこから右の方に目を移すと、50分過ぎでは線が交差しまくって、ゴールド差と勝率がほとんど関係しなさそうな雰囲気を出しています。
そこで、雰囲気ではなく本当に勝率に違いが無いのかを調べるために、1000G差と2000G差、2000G差と3000G差と言った隣り合う系列のデータの組に関して1分毎のデータごとにカイ二乗検定を行いました。カイ二乗検定を簡単に説明すると、1000G差と2000G差で勝率が変わらない、という仮説がどれだけ妥当か調べる方法です。1000G差と2000G差で勝率が変わらないという仮説が妥当ではない、という結果が出たらその2つには勝率に違いがあるといえます。
検定の結果15000G差と10000G差は34分では2つに勝率の違いがあるが、35分の時点で勝率に違いがないとは言えない、という結果が出ました。これらをまとめたものが表3です。

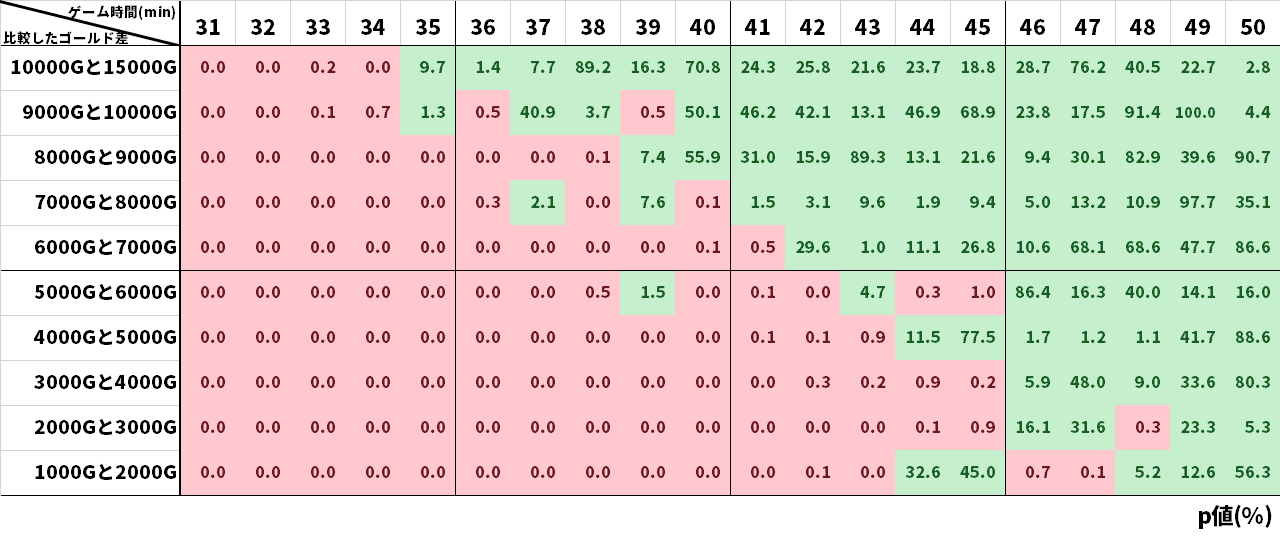
この表の見方を説明すると、赤いマスの所は横のゴ－ルド差と縦の時間の時、勝率に違いがあり、緑のところは勝率に違いが無い、という結果になったということです。「10000Gと15000G」に注目すると34分までは赤いので10000G差と15000G差の2つには勝率の違いがありますが、緑になった35分以降は10000G差でも15000G差でも勝率に違いが無い、という検定結果になりました。
この表の緑と赤の境界線に注目すると、それは右肩下がりになっています。ということは、大きなゴールド差同士、15000G差の勝率と10000G差の勝率は35分に違いが無くなり、それ以降ゴールド差が大きいほうから順に、時間経過で勝率の違いが無くなっているということです。最終的に48分までに全ての組で勝率に違いがあるとは言えない結果になりました。つまり、35分ごろでは2000G差と3000G差では勝率の違いが7~8%あったにもかかわらず、48分にはそれが無くなってしまった、ということです。

そして、56分以降ではゴールド差がいくつであっても勝率が50%より大きいとは言えない結果になりました。（表4）

実験2の議論：検定結果の解釈方法

これらの統計的検定の結果をどう解釈すべきかということですが、数字に関して厳密にとらえるよりも、傾向が出ていると考えるべきです。つまり、表4に関しては「ゴールド差がいくつであっても勝率が50%より大きいとは言えなくなる境界は56分である」ではなく「ゴールド差がいくつであっても勝率が50%より大きいとは言えなくなる境界は56分『付近』にある」という風に解釈すべきだと考えました。理由は、統計はあくまで分析した一部のデータから、全体を予想しようとするものです。違うデータや違うパッチで完全に同様の検討を行ったとしても、同じ数字が出るとは限りません。なので、今回だけの結果を持って、「56分」以降にゴールド差がいくつであっても勝率が50%になる、言い切ってしまうと「本当に56分?55分や57分ではなく?」という疑問があるからです。一方で、どれだけ差があろうともこの時間帯になってしまえば、負けているチームもフルビルドになり、ビルドではほとんど差が無くなると考えられます。なので、今回の結果はゲームのルール、システムから考えると非常に妥当な結果に見えます。
以上をまとめると、56分という数字を言い切ってしまうと間違った結論に達してしまう可能性があります。しかし56分周辺にゴールド差に関係なく勝率が50%になる境界線がありそうです。これらのことから、今回の実験の結論は「ゴールド差がいくつであっても勝率が50%より大きいとは言えなくなる境界は56分付近にある」というものにしました。
表3に関しても、統計の限界から本当は赤になるべきなのに緑になっているマス（逆に本当は緑なのに赤になっているマス）がいくつかある可能性が高く、そう考えると○○分でゴールド差と勝率が関係無くなると断定することは間違った結論に行きかねません。しかし、全体の傾向は出ていると考えています。なので、数字、特に時間に関しては断定的に表現しないのが妥当だと考えます。以上をまとめた結論は以下のようになります。